69 二叉树的线索化实现
二叉树的线索化实现(一)
-
什么是线索化二叉树?
- 将二叉树转换为双向链表的过程(非线性->线性)
- 能够反映某种二叉树的遍历次序(结点的先后访问次序)
- 利用结点的right指针指向遍历中的后继结点
- 利用结点的left指针指向遍历中的前驱结点
-
如何对二叉树进行线索化?
思维过程 :线索化能够反映遍历次序→线索化算法必然与遍历算法相关→如何在遍历时记录结点间的访问次序→使用队列(先进先出)→遍历结束后,队列记录了访问次序→循环访问队列,连接队列中的结点
-
二叉树的线索化
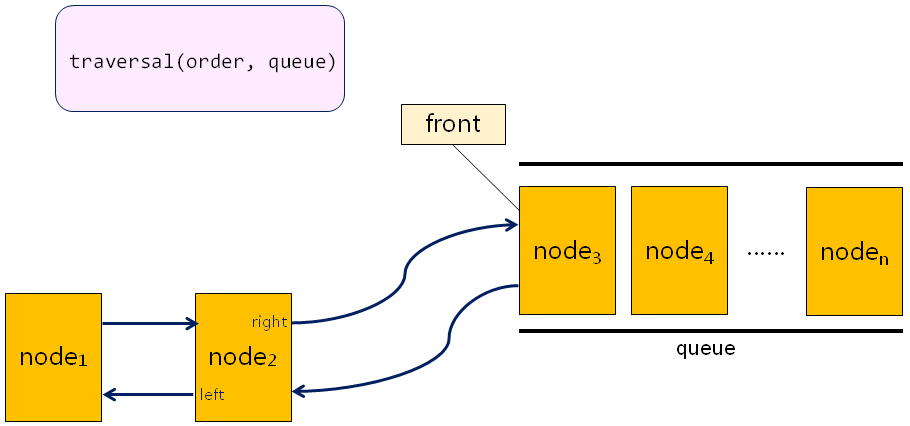
-
目标
- 新增功能函数traversal(order,queue)
- 新增遍历方式BTTraversal::LevelOrder
- 新增公有函数BTreeNode* thread(BTTraversal order)
- 消除遍历和线索化的代码冗余(代码重构)
编程实验(一)
-
新增加功能函数
二叉树的线索化实现(二)
-
层次遍历算法小结
- 将根结点压入队列中
- 访问队头元素指向的二叉树结点
- 队头元素弹出,将队头元素的孩子压入队列中
- 判断队列是否为空(非空:转2,空:结束)
-
层次遍历算法示例
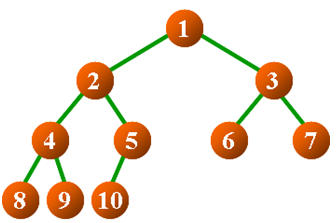
循环 tmp队列 queue队列 初始 1 - i = 1 2,3 1 i = 2 3,4,5 1,2 i = 3 4,5,6,7 1,2,3 i = 4 5,6,7,8,9 1,2,3,4 i = 5 6,7,8,9,10 1,2,3,4,5 i = 6 7,8,9,10 1,2,3,4,5,6 i = 7 8,9,10 1,2,3,4,5,6,7 i = 8 9,10 1,2,3,4,5,6,7,8 ... ... ... 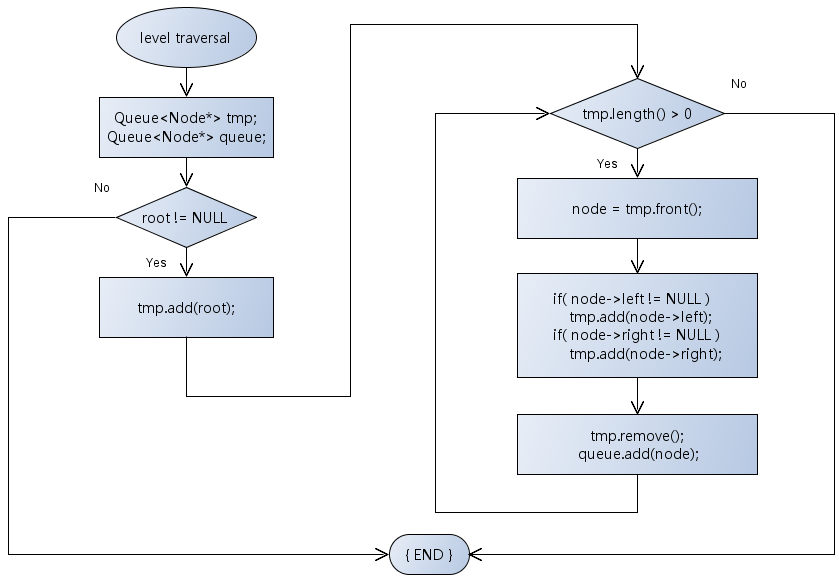
编程实验(二)
-
层次遍历算法
二叉树的线索化实现(三)
-
函数接口设计
BTreeNode *thread(BTTraversal order)- 根据参数order选择线索化的次序(先序,中序,后序,层次)
- 返回线索化之后指向链表首结点的指针
- 线索化执行结束之后对应的二叉树变为空树
-
线索化流程
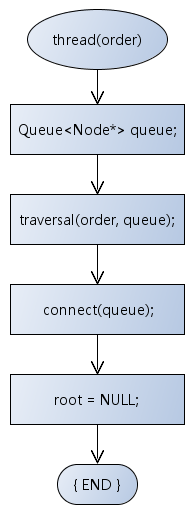
-
队列中结点的连接算法[connect(queue)]
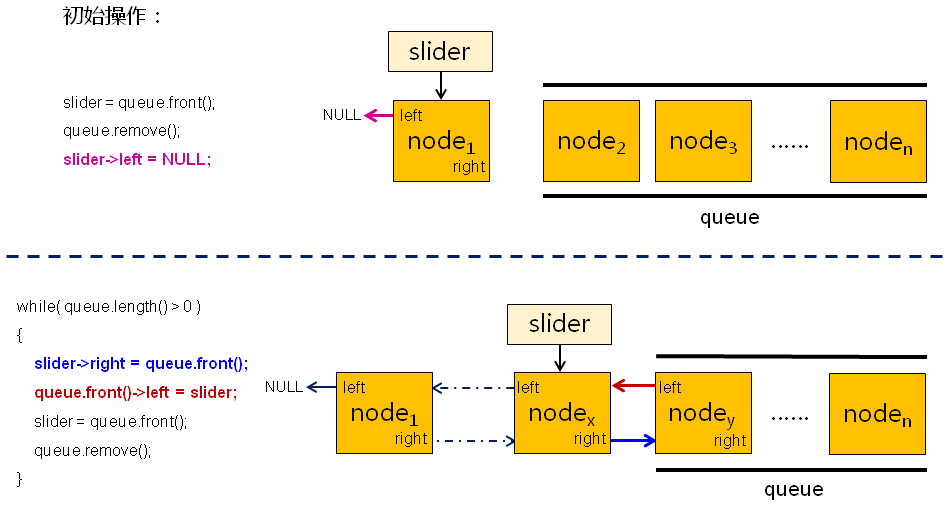
编程实验(三)
-
二叉树的线索化
小结
- 线索化是将二叉树转换为双向链表的过程
- 线索化之后结点间的先后次序符合某种遍历次序
- 线索化操作将破坏原二叉树结点间的父子关系
- 线索化之后二叉树将不再管理结点的生命期
70 二叉树的经典面试题分析
-
面试题一
- 单度节点删除
- 编写一个函数用于删除二叉树中所有单度结点
- 要求:结点删除后,其唯一的子结点替代它的位置
- 单度节点删除
-
结点中包含指向父结点的指针
- 定义功能:delOdd1(node)
- 删除node为根结点的二叉树中的单度结点

- 定义功能:delOdd1(node)
编程实验
-
单度结点删除一
-
结点中只包含左右孩子的指针
- 定义功能:delOdd2(node) //node为结点指针的引用
- 删除node为根结点的二叉树中的单度结点

- 定义功能:delOdd2(node) //node为结点指针的引用
编程实验
-
单度结点删除二
-
面试题二
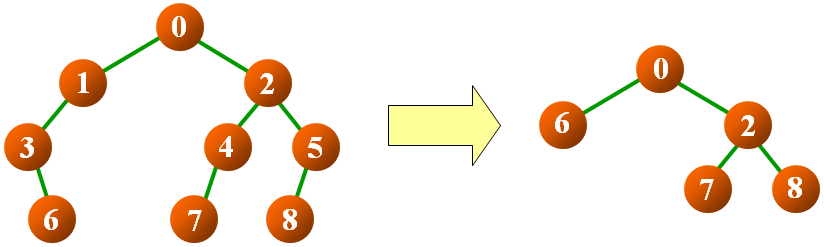
- 中序线索化二叉树
- 编写一个函数用于中序线索化二叉树
- 要求:不允许使用其它数据结构
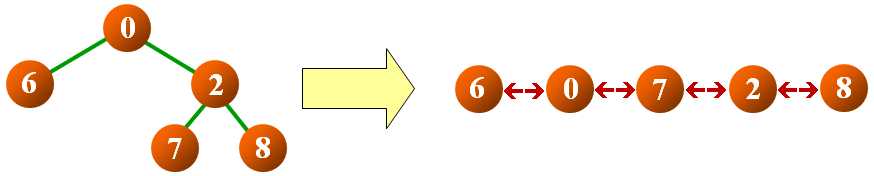
- 中序线索化二叉树
-
解法一:在中序遍历的同时进行线索化
- 思路:
- 使用辅助指针,在中序遍历时指向当前结点的前驱结点
- 访问当前结点时,连接与前驱结点的先后次序
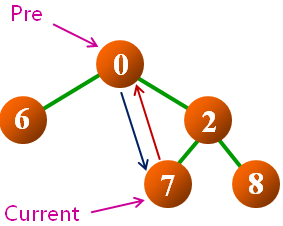
- 思路:
-
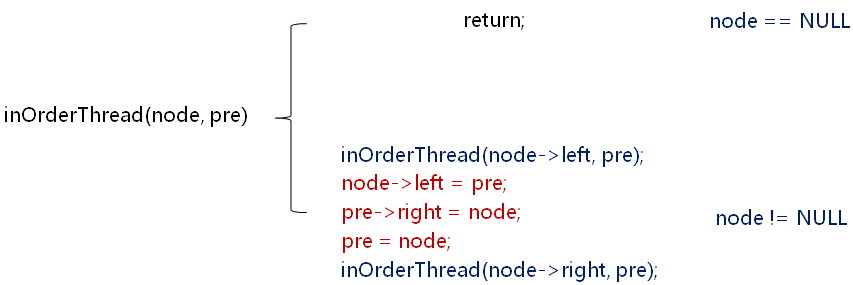
定义功能:inOrderThread(node,pre)
- node:根结点,也是中序访问的结点
- pre:为中序遍历时的前驱结点指针
编程实验
-
中序线索化一
-
解法二:中序遍历的结点次序正好是结点的水平次序
- 思路:
- 使用辅助指针,指向转换后双向链表的头结点和尾结点
- 根结点与左右子树转换的双向链表链接,成为完整双向链表
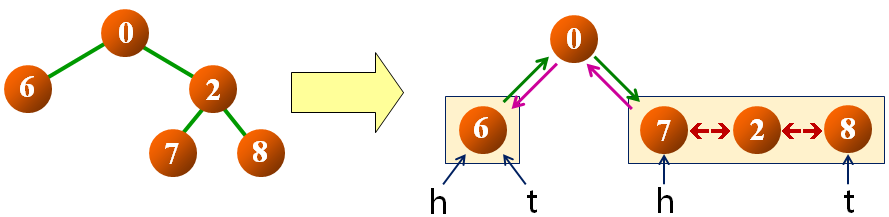
- 思路:
-
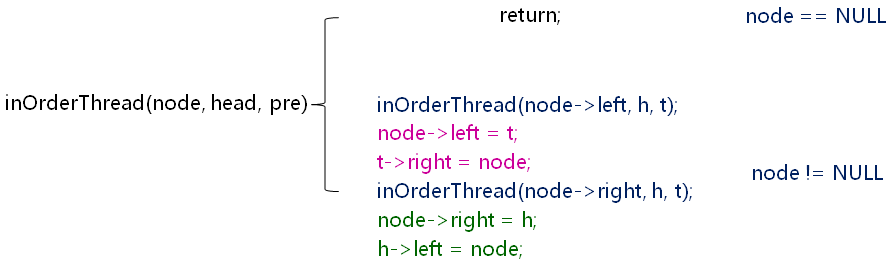
定义功能:inOrderThread(node,head,tail)
- node:根结点,也是中序访问的结点
- head:转换成功后指向双向链表的首结点
- tail:转换成功后指向双向链表的尾结点
编程实验
-
中序线索化二